Polyalphabetic substitution and Transposition Ciphers

1. Using polyalphabetic substitution, with alphabet a–z (no caps), spaces translated to an underscore character (_), and a period (., as the last character of the alphabet), use the private key security to encrypt the plaintext message:

    send_money
   

   To help you, use the following formula:

   Encryption: ciphertext = (plaintext + key) mod 28
   
   Decryption: plaintext = (ciphertext - key) mod 28
   

   Number your alphabet so that it starts with zero, e.g., A = 0, Z=25, _ = 26, . = 27. This means that your alphabet will be abcdefghijklmnopqrstuvwxyz_.

   As a general rule for shift ciphers, the modulus is always the size of the alphabet, but you must start your alphabet at 0.

   To check your understanding of modular arithmetic, review these examples on wikipedia.

   You may use an online vignere cipher calculator to check your work. If you use this calculator, remember to customize the default alphabet to include periods and underscores.

   Heads up! You should understand this well enough to be able to do it by hand.
   Question : What is the ciphertext when encrypting “send_money” with the key “security” and alphabet abcdefghijklmnopqrstuvwxyz_.?

2. Consider the transposition method discussed in class. Assume the plaintext is

   attack postponed until two am
   

   and the key is security

   Create the ciphertext using columnar transposition (demonstrated in class). Remove spaces from the plaintext.

   You may use an online columnar transposition calculator to check your work.

   Heads up! You should understand this well enough to be able to do it by hand.
   Question : What is the ciphertext when encrypting “attack postponed until two am” with the provided key?

Frequency analysis

Perform frequency analysis on the following ciphertext. You may use an online frequency analysis tool such as this one .

Hvs Qosgof qwdvsf wg boasr othsf Xizwig Qosgof, kvc, oqqcfrwbu hc Gishcbwig, igsr wh kwhv o gvwth ct hvfss hc dfchsqh asggousg ct awzwhofm gwubwtwqobqs. Kvwzs Qosgof'g kog hvs twfgh fsqcfrsr igs ct hvwg gqvsas, chvsf gipghwhihwcb qwdvsfg ofs ybckb hc vojs pssb igsr sofzwsf.

Wt vs vor obmhvwbu qcbtwrsbhwoz hc gom, vs kfchs wh wb qwdvsf, hvoh wg, pm gc qvobuwbu hvs cfrsf ct hvs zshhsfg ct hvs ozdvopsh, hvoh bch o kcfr qcizr ps aors cih. Wt obmcbs kwgvsg hc rsqwdvsf hvsgs, obr ush oh hvswf asobwbu, vs aigh gipghwhihs hvs tcifhv zshhsf ct hvs ozdvopsh, boaszm R, tcf O, obr gc kwhv hvs chvsfg.
—Gishcbwig, Zwts ct Xizwig Qosgof 56

Vwg bsdvsk, Oiuighig, ozgc igsr hvs qwdvsf, pih kwhv o fwuvh gvwth ct cbs, obr wh rwr bch kfod ofcibr hc hvs psuwbbwbu ct hvs ozdvopsh:
Kvsbsjsf vs kfchs wb qwdvsf, vs kfchs P tcf O, Q tcf P, obr hvs fsgh ct hvs zshhsfg cb hvs goas dfwbqwdzs, igwbu OO tcf L.
—Gishcbwig, Zwts ct Oiuighig 88

Hvsfs wg sjwrsbqs hvoh Xizwig Qosgof igsr acfs qcadzwqohsr gmghsag og kszz, obr cbs kfwhsf, Oizig Uszzwig, fstsfg hc o (bck zcgh) hfsohwgs cb vwg qwdvsfg:
Hvsfs wg sjsb o fohvsf wbusbwcigzm kfwhhsb hfsohwgs pm hvs ufoaaofwob Dfcpig qcbqsfbwbu hvs gsqfsh asobwbu ct zshhsfg wb hvs qcadcgwhwcb ct Qosgof'g sdwghzsg.
—Oizig Uszzwig, Ohhwq Bwuvhg

Wh wg ibybckb vck sttsqhwjs hvs Qosgof qwdvsf kog oh hvs hwas, pih wh wg zwyszm hc vojs pssb fsogcbopzm gsqifs, bch zsogh psqoigs acgh ct Qosgof'g sbsawsg kcizr vojs pssb wzzwhsfohs obr chvsfg kcizr vojs oggiasr hvoh hvs asggousg ksfs kfwhhsb wb ob ibybckb tcfswub zobuious. Hvsfs wg bc fsqcfr oh hvoh hwas ct obm hsqvbweisg tcf hvs gczihwcb ct gwadzs gipghwhihwcb qwdvsfg. Hvs sofzwsgh gifjwjwbu fsqcfrg rohs hc hvs 9hv qsbhifm kcfyg ct Oz-Ywbrw wb hvs Ofop kcfzr kwhv hvs rwgqcjsfm ct tfseisbqm obozmgwg.

Qosgsf_qwdvsf, Kwywdsrwo

Questions:

1. What are the four most frequent characters, in descending order? Examine the frequency table chart at http://en.wikipedia.org/wiki/Frequency_analysis. What does this suggest the four letters identified correspond to?

   Question : What are the four most frequent characters?

2. Analyze bigrams and trigrams in the ciphertext.

   What do the most frequent ciphertext bigrams suggest the three 2-length N-grams identified correspond to in English plaintext?

   Also examine N-grams of length 3, and report the likely plaintext identities of the four 3-length N-grams reported. (Use http://en.wikipedia.org/wiki/Trigram).

   Question : What are the three most frequent trigrams?

3. Assume that a simple cipher that shifts all characters by a fixed number was used to create the cipertext (a caesar cipher). Given the results of the frequency analysis, what would the shift key have been (the shift to go from plaintext to ciphertext)? Don’t be proud; you can use your fingers to count.

   Question : What is the key of the ciphertext, counting forwards?

4. What is the plaintext?

   Hint: You can use an online caesar cipher encoder/decoder such as this one to test your key, although you should be able to perform frequency analysis by hand on short texts.

   Question : What author is quoted in the plaintext?

One-time Pad

Decrypt the following ciphertext using the following one-time pads, using an XOR bitwise operation.

You may use an online tool such as cryptii.com. For example, select “bitwise operation”:

And then choose “XOR”, leaving the operation on “encode”:

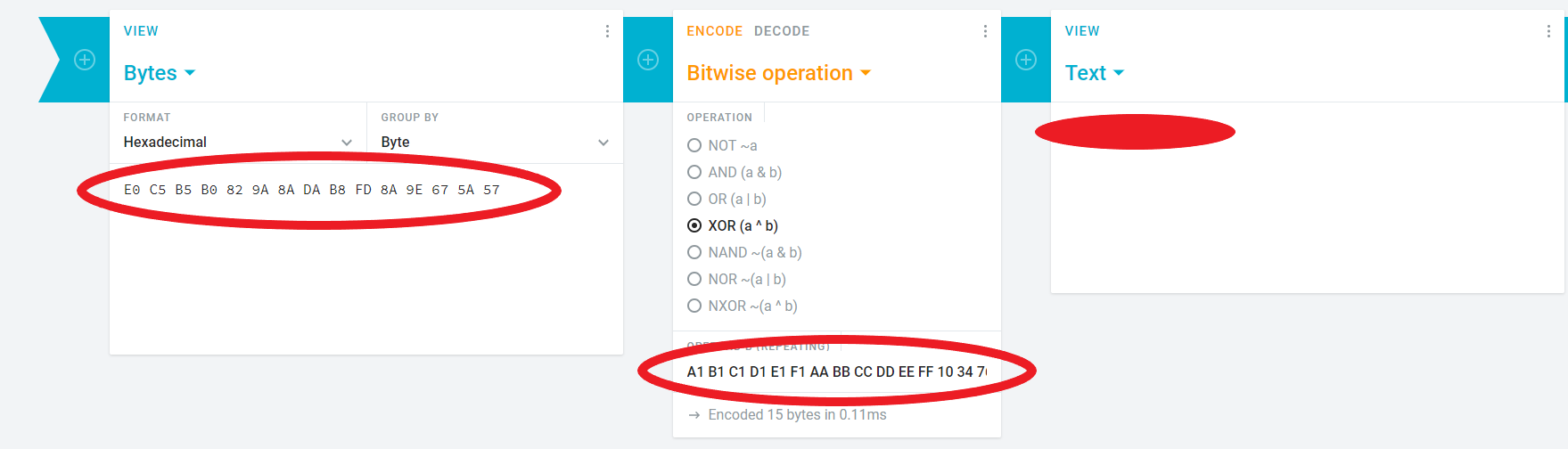
Ciphertext (hexadecimal): E0 C5 B5 B0 82 9A 8A DA B8 FD 8A 9E 67 5A 57

1. One-time pad 1: A1 B1 C1 D1 E1 F1 AA BB CC DD EE FF 10 34 76

   Question : What is the plaintext using the one-time pad 1?

2. One-time pad 2: B2 A0 C1 C2 E7 FB FE FA D9 89 AA AF 56 6A 67

   Question : What is the plaintext using the one-time pad 2?

3. One-time pad 3: B3 B0 C7 C2 E7 F4 EE BF CA DD EC F1 15 2E 76

   Question : What is the plaintext using the one-time pad 3?

4. One-time pad 4: B4 AD D0 90 E1 FB FE FA D1 8E AA FA 02 3B 33

   Question : What is the plaintext using the one-time pad 4?

Hashing

Hash the following plaintext using multiple hashing algorithms.

We intend to begin on the first of February unrestricted submarine warfare.
We shall endeavor in spite of this to keep the United States of America neutral.
In the event of this not succeeding, we make Mexico a proposal of alliance on
the following basis: make war together, make peace together, generous financial
support and an understanding on our part that Mexico is to reconquer the lost
territory in Texas, New Mexico, and Arizona. The settlement in detail is left to
you. You will inform the President of the above most secretly as soon as the
outbreak of war with the United States of America is certain, and add the
suggestion that he should, on his own initiative, invite Japan to immediate
adherence and at the same time mediate between Japan and ourselves. Please call
the President's attention to the fact that the ruthless employment of our
submarines now offers the prospect of compelling England in a few months to
make peace.

Signed, ZIMMERMANN

You may use a tool such as cryptii.com. For example, select “Hash function” from towards the bottom of the menu:

And use it as follows:

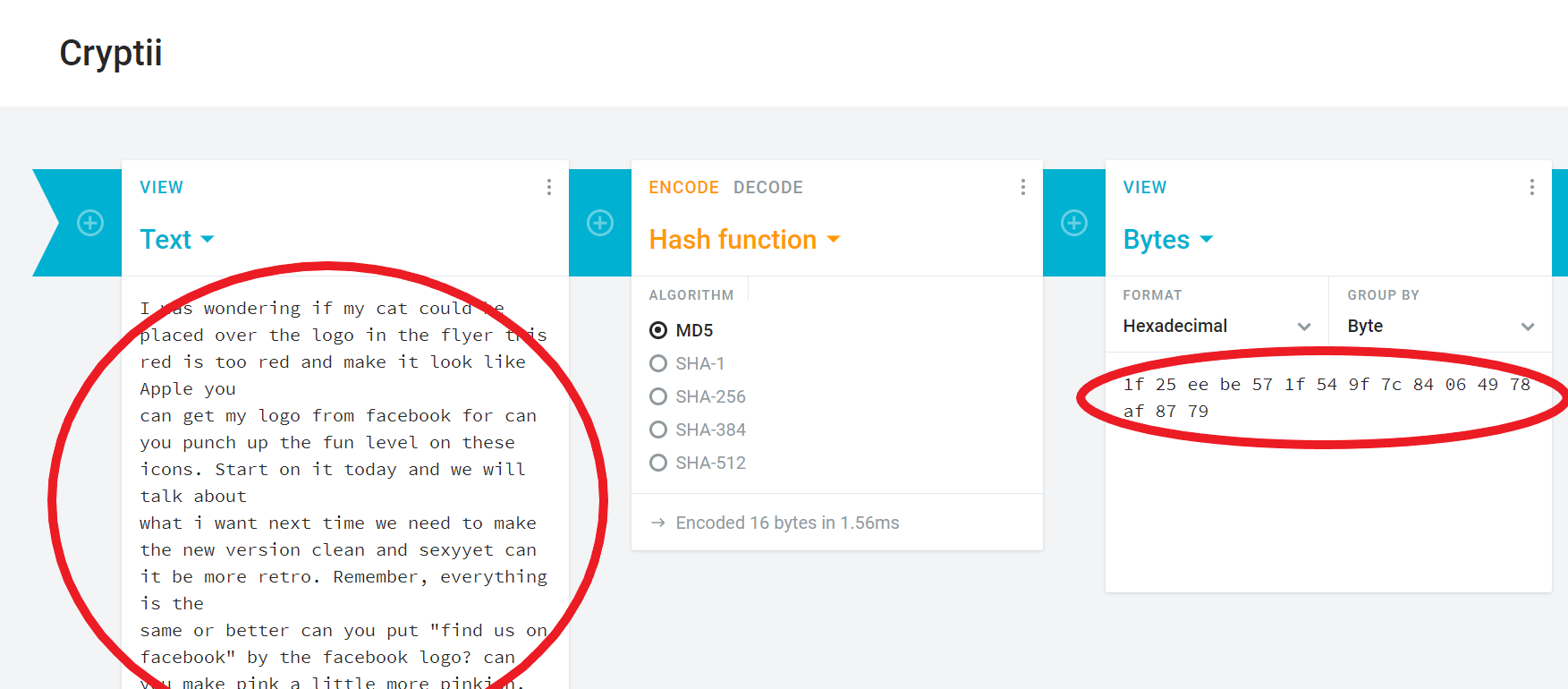
Questions:

1. What is the length of each of the following algorithm hashes in bytes? MD5, SHA-1, SHA-256, SHA-512? How many bits does each hash represent?

   (hint: how many bits are in one hex digit – also called a ‘nibble’? How many nibbles in the key? Or, How many bits in a byte, and how many bytes in a two-digit hex number like ‘FA’? Review this if you’re still stuck)

   Question : How many bits are in an MD5 hash?

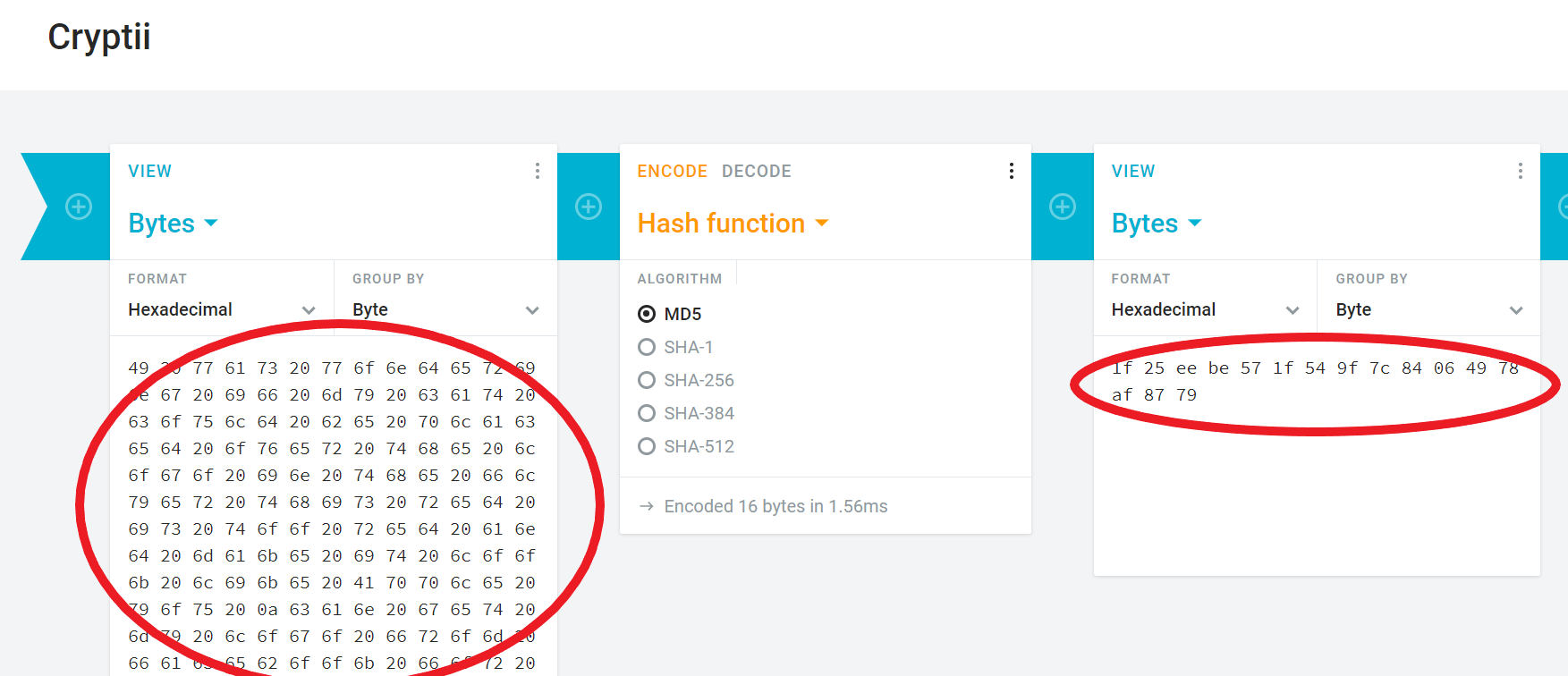
Change just a single bit in content that you are hashing. e.g, change an “A” — 1010 to a B — 1011. Examine the hashes of the modified content. Since you only changed a single bit in a file of billions of bits, you might reason that the hashes would be nearly the same. Are they?

In cryptii, you can switch to a hex view thusly in order to make your single-bit-edit easier:

Symmetric encryption with AES

Decrypt the message below using AES and the following parameters: Message (base64):

K2NsjCqFlnNVFK1dTTm/opzc0Fq+qNj8UVg+nvIzeEgv5Y3GHATcnyROU6eg+6BAesm5qrtZe5vdjP+ffI/vYIEqIxZh9CSCbxBCo2HEYjbOFCIkx3OuoaomxGChwwbRS2lX37prQMR3VYKVXvQoLUPocPXn+oxnqqHXS/2JbLkTlOje6mrLhnjlI6VDkGDMZI3WqWRe5aHNyzQTEdhXbizHGcKrk/JpX7L1ODY0gdw6InhXew5c4EEcqQInONbYel8W5xwPYFojsKTbKRAOrNqIfI46vD9ziAFCbkG10aIRzLJmxQrkiX+DPwjuxC/p97C9Rm9DS2zn4Yy1mZCFalVDk2MLfgRtW2MBpHDHV1FGdhusnH1E0WNaOfTKlU5tyh3ImBEHS0VBlv3wEEm9f2MVyxK/0T6JdfHD/Szf1yj0GNNMGeKTpmPjP0lmwVdo5GkJJsVBPAWzGqeI+q9phUGw6YC7f4NvlT/RiyOoM8aFAwJxA7MsKTFxyv9ib47pYC8YfOJPpnuGiHw2GutS1/z3TIk40ABFcjyc3R5AxNKM3wJjRWNwrCy9ruva/kddEMa6ANIwLYO0RuTwplU00QFUaggUtYPoPur4nT1sEoY=

• Algorithm: AES-256
• Chaining mode: CBC
• IV (hexadecimal): 15 7F 14 FF DF D1 D4 25 D9 CB BD 12 ED 98 49 2F
• Key (hexadecimal): FA 71 7D 51 3F D7 32 7D D9 C7 13 84 43 47 C2 5B 2F 9C 1E 48 67 C6 81 32 85 5A 13 92 60 A8 79 44

You can do this on cryptii using the “Block Cipher” tool. To do so:

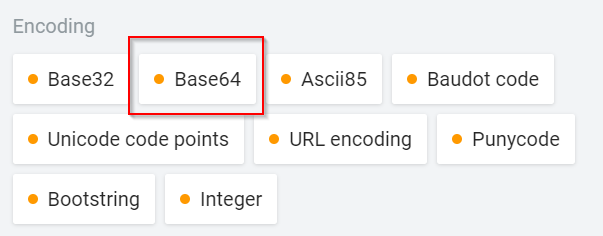
1. Start by selecting the “Encoding > Base64” tool.

   
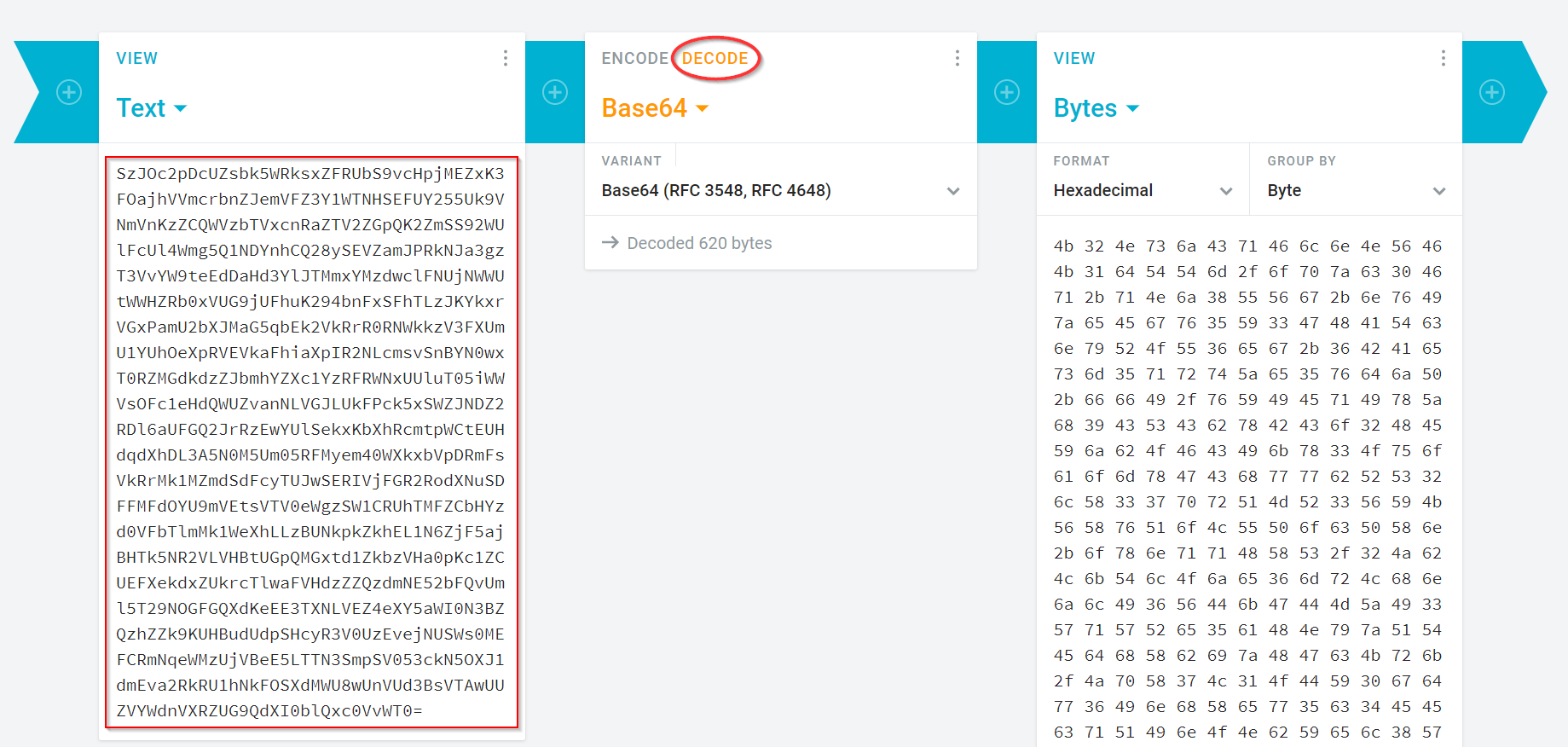
2. Set the base64 to “decode” mode.

3. Paste the above base64-encoded string into the leftmost “text” node. Make sure there are no extra characters after the final = in the pasted value (not even a return character!).

   The output of the base64 tool will be bytes.

   

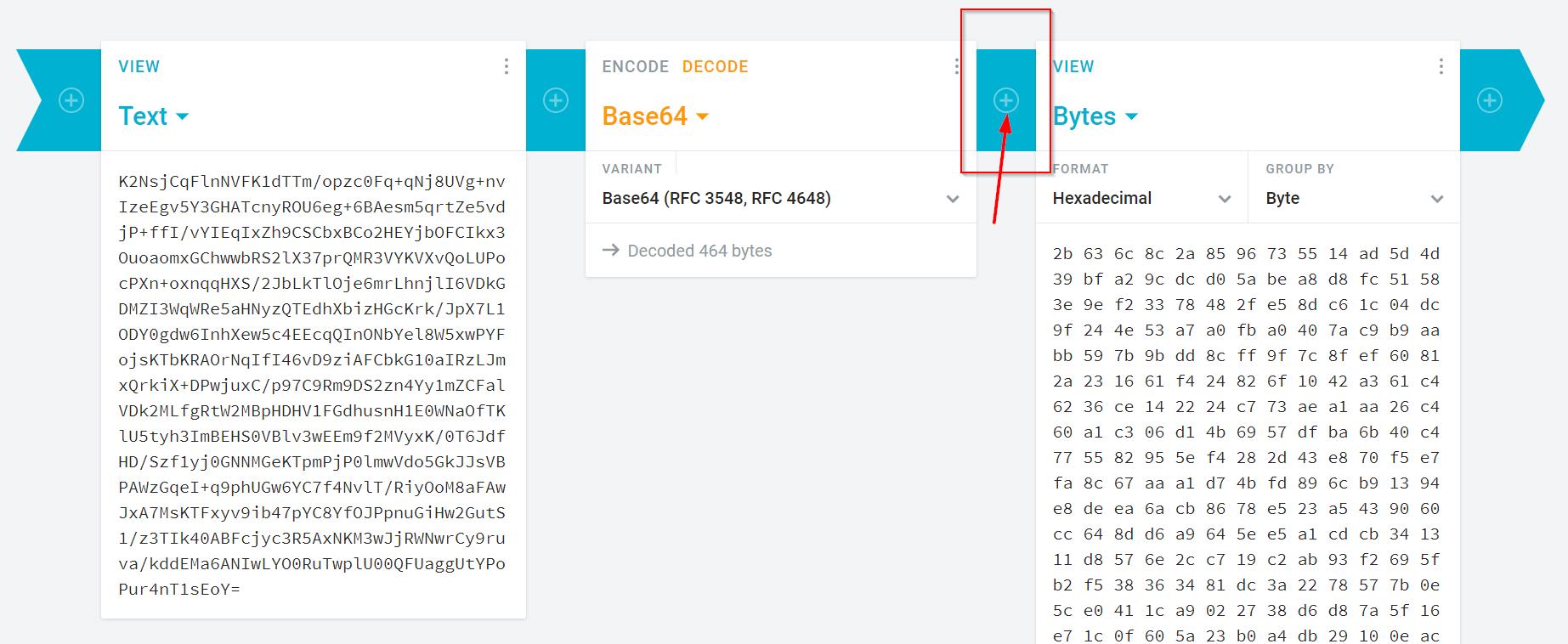
4. Add a “Modern Cryptography > Block Cipher” tool to the flow, so that the bytes flow into it. Set the block cipher tool to use AES-256, and use the algorithm settings noted above.

   
   

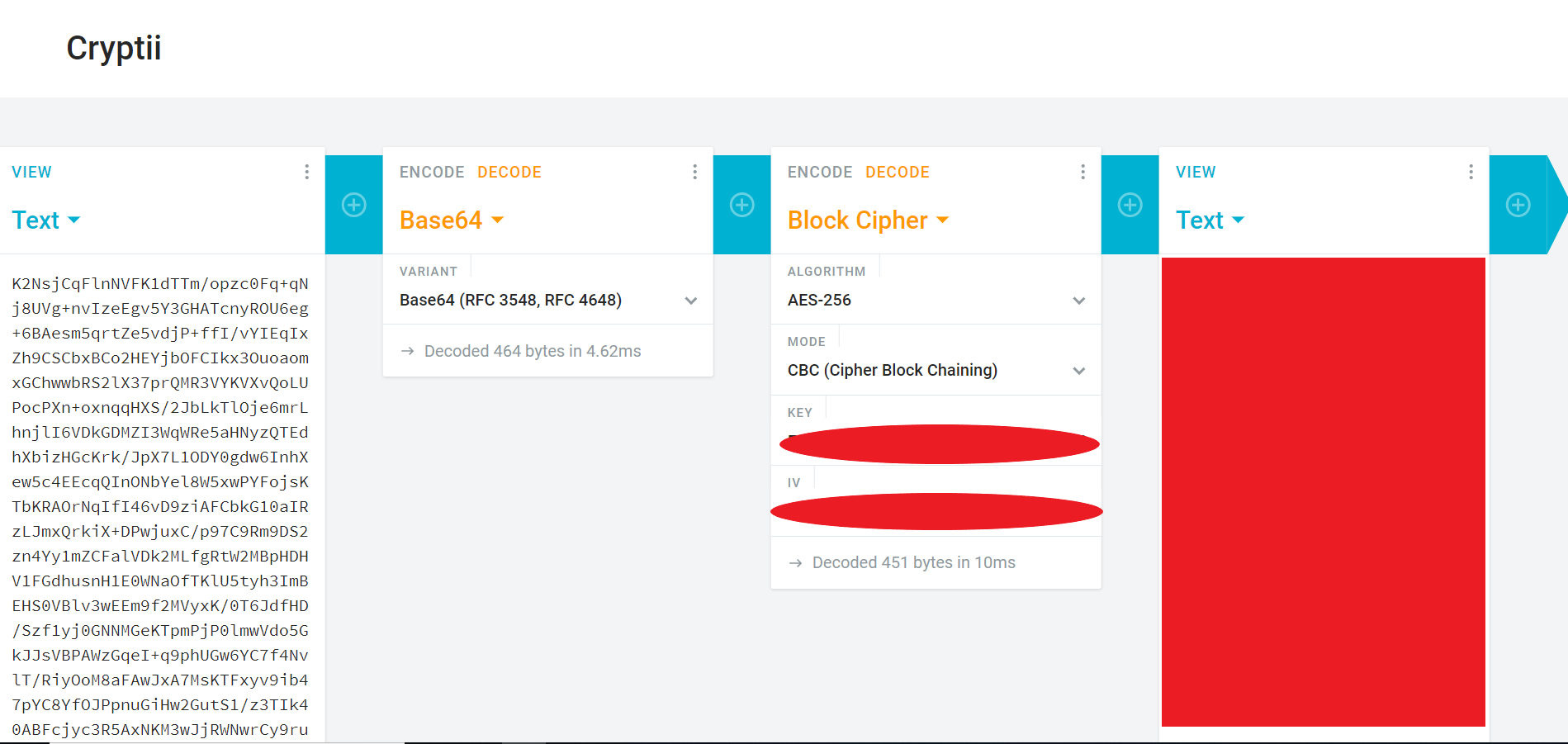
What is the plaintext of the message?

Message Sharing

Use AES or another symmetric block cipher to encrypt/decrypt messages exchanged between you and another class member. You can use a site such as cryptii.com.

You and your classmate should agree on a password for encrypting the message. You can generate a key and an IV from a password using the openssl tool, available from your Kali instance. For example, if you had agreed on the password Password1, you could run the following to get the corresponding key and IV:

openssl enc -aes-256-cbc -P -pass pass:Password1 -nosalt

Running the above will give the same output every time. It would lead to the following output:

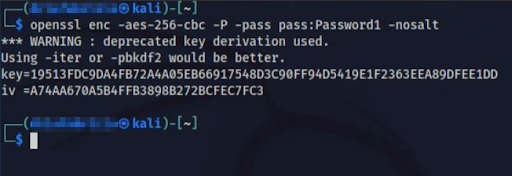
Where:

• enc tells openssl to use its symmetric cipher routines
• the block cipher is aes cbc with a block size of 256
• the password from which the key and IV are derived is Password1
  • (in real life, please never use a password this weak!)
• -nosalt tells openssl to not introduce randomness into the process of generating a key and IV from a password (in practice, you should let it use a salt – more on this in a future lab)

• -P tells openssl to:

  -P  print out the key and IV used then immediately exit: don't do any encryption or decryption.
  

  (see man enc)

You and your classmate should agree on a password, then use that password to share a message using AES.

Questions:

• Question : How did you ensure that your key exchange was safe? How would you exchange keys if you were not in the same location?
• Question : Which of the parameters of a block cipher (e.g., algorithm name, mode of operation, IV (if any), key length) are essential to keep secret? Security through obscurity does not count as “essential”.

Deliverable

Submit your answers for this lab by completing the associated lab quiz on your course’s learning management system.