Lab: Asymmetric Encryption
Understanding asymmetric encryption and RSA practice
Part 1. Understanding Asymmetric Keys
-
Key Exchange Problem.
Imagine 200 people wish to communicate securely using symmetric keys, one symmetric key for each pair of people. (See Metcalf’s Law).
Question : How many symmetric keys would this system use in total? -
RSA keys vs AES keys.
Review keylength.com, which gives estimates for good key lengths.
The below screenshot from the site shows example output comparing different organization recommendations specifying the date “2030”.
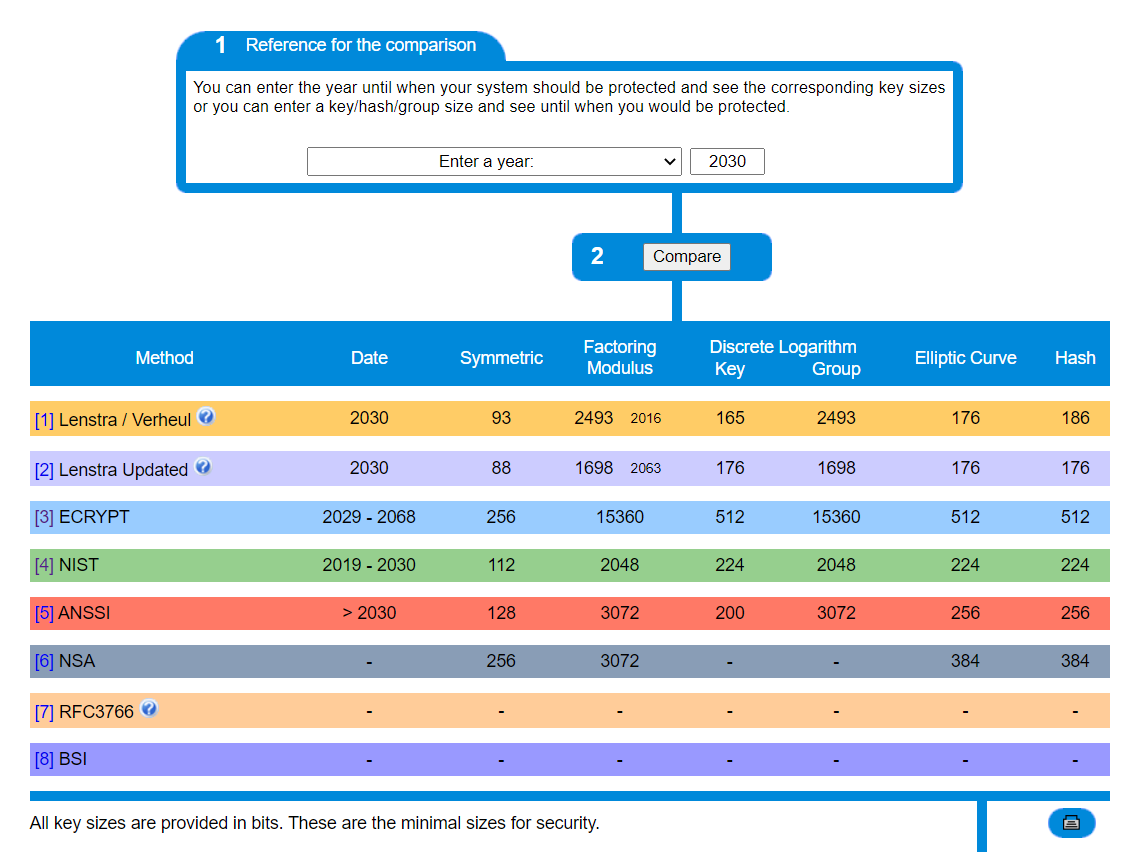
Here are some tips for interpreting what is shown:
- “Method”: The site lists key length recommendations from multiple organizations, including from NIST.
- “Date” means how long you’ll be secure until, using the given algorithm-keylengths.
- Key lengths for multiple cryptography algorithmic approaches and applications are shown.
- “Symmetric” algorithms include AES.
- “Factoring Modulus” applies to asymmetric algorithms such as RSA.
- “Discrete Logarithm” refers to asymmetric algorithms such as Diffie Hellman (DH).
- “Elliptic Curve” (EC) is a variant of Discrete Logarithm algorithms, and is therefore also an asymmetric algorithm. EC variants of DH exist.
- “Hash” refers to algorithms such as the SHA family.
Question : Does a 256-bit RSA key (a key with a 256-bit modulus) provide strength similar to that of a 256-bit AES key? Explain.
Part 2. Calculating RSA keys
To help you answer the following questions, view this “RSA Algorithm” video. Also, you can review the RSA wikipedia page example.
You can use a calculator such as WolframAlpha to help with this modular arithmetic. But you should understand the principles well enough to perform them by hand with simple problems.
-
Use RSA to encrypt
M=9to cipertext and back again to plaintext usingp=5, q=11, e=3. Show your work.Question : What is the ciphertextCwhen using RSA to encryptM=9withp=5, q=11, e=3?Question : Show your work both for encrypting the message (M=>C), and also for decrypting the message back (C=>M) -
You are Eve. In a public-key system using RSA, you intercept the ciphertext
C=10sent to a user whose public key ise=5, n=35. Decrypt the cipertext.Question : What is the plaintextMgivenC=10, e=5, n=35?
Deliverable
Submit your answers for this lab by completing the associated lab quiz on your course’s learning management system.